|
In the local differential geometry, the Frenet-Serret frame has the basic importance
to investigate characterizations of the curves. For instance, curvature functions give us
the behavior of the curves. In local differential geometry, we think of curves as a geometric
set of points or locus. Therefore, investigating Frenet-Serret frame of the curve is a
classical aim to determine its behavior. There is an extensive literature on the subject, for
instance, in Ma_2OE1.JPG) gden (1990), the author presented a method to calculate Frenet-Serret apparatus
of the regular curves in the Euclidean 4-space. Thereafter, Yilmaz (2001), adapted this
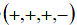method to spacelike curves of Minkowski 4-space according to signature and investigated spherical images of such curves. However, in the existing literature, the works were
commonly based on the spacelike and timelike curves of Minkowski space-time with
signature 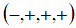 . Since, in Yilmaz and Turgut (2008) and Yilmaz et al. (2009), respectively, the mentioned method (originally expressed as in  was adapted and
developed for spacelike and timelike curves of Minkowski space-time. Recently, in Turgut et al. (2009), the same idea is studied for non-null curves of Lorentzian 5-space by the spirit of the
paper (Yilmaz and Turgut, 2008). Einstein's theory opened a door to using new geometries
and thus, the researchers discovered a bridge between modern differential geometry
and mathematical physics. Generally they used the concepts of a mapping and a curve.
For instance, a `particle' in special relativity means a curve with a timelike unitary
tangent vector, for details (Caltenco et
al., 2002); and in another work, it has also been
observed that the third curvature is important (Kichenassamy, 2003). Thereafter, null cases were
also studied to make an understanding tool of general relativity as a dynamical theory and
the Frenet-Serret formalism and by this way black holes were investigated in five and
six dimensional space by considering a timelike curve (Iyer and Vishveshwara, 1988; and
Capovilla et al., 2006). However, this paper did not include an explicit calculation of
Frenet-Serret frame with a vector derived from a generalization of cross product in Lorentzian space.
A curve of constant slope or general helix is defined by the property that the tangent
lines make a constant angle with a fixed direction. A necessary and sufficient condition that
a curve to be a general helix in Minkowski 3-space is that the ratio of curvature to torsion
be constant (Ferrnández et al., 2001). Indeed, a helix is a special case of the general helix.
If both curvature and torsion are non-zero constants, it is called a helix or only a
W-curve 
Helices arise in nanosprings, carbon
nanotubes, a-helices, DNA double and collagen triple helix, the double helix shape is commonly
associated with DNA, since the double helix is the structure of DNA (Camci et al., 2009). This fact was first published by Watson and Crick (1953). They constructed a molecular model of DNA
in which there were two complementary, antiparallel (side-by-side in opposite directions)
strands of the bases guanine, adenine, thymine and cytosine, covalently linked
through phosphodiesterase bonds (Cook, 1979; Chouaieb et al., 2006; and Camci et al., 2009). In
this work, we extend the notion of calculate Frenet-Serret apparatus of helices
(W-curves) considering the paper of Yilmaz and Turgut (2009) which contains regular observations
of helices in six dimensional Euclidean space. Additionally, we express an example of our
main results. We hope these results will be helpful to mathematicians who are specialized
in mathematical modeling.
|
