Systemic Liquidity Risk: A Macroeconomic Evaluation

Ashish Srivastava
AGM and Member of Faculty,
College of Agricultural Banking,
Reserve Bank of India,
University Road, Pune 411016, Maharashtra,
India. E-mail: ashishsrivastava@rbi.org.in

Stock market volatility has always been an area of concern for market participants and policy regulators. Through this paper, an attempt has been made to model the volatility in the Indian equity market by employing the standard GARCH(1, 1) model. The paper also investigates whether the volatility on NSE has changed after the introduction of Volatility Index (India VIX) through the GARCH(1, 1) model with a dummy. Accordingly, the period of study for measuring the volatility has been split into two, i.e., the pre-IVIX introduction period (January 1, 2000 to October 31, 2007) and the post-IVIX introduction period (November 1, 2007 to August 31, 2016). The results of GARCH(1, 1) model with a dummy reveal that the volatility of the spot market has declined after the introduction of IVIX in India. In addition, the results of standard GARCH(1, 1) models provide evidence that recent news has a greater impact on the spot market changes in the post-IVIX introduction period.

Introduction

Systemic liquidity risk has attracted the attention of the financial sector beyond the corridors of central banking, especially in the aftermath of the global financial crisis. However, it has not gained as much significance in the spectrum of risk management as it should have, given the enormity of its impact, and it has continued to be seen as a monetary policy or lender of last resort (LOLR) function. The challenge posed by the systemic liquidity risk is that even perfectly rational liquidity management decisions taken at the level of an individual financial institution could prove hazardous at the systemic level. Hence, it is important to understand the causal relationships between the macroeconomic variables impinging upon the systemic liquidity. There is an ongoing debate on how to adequately address the systemic component of the liquidity risk and a number of researchers have studied its various dimensions. Maddaloni (2015) noted that risk stemming from the bank's liquidity management inefficiency or strategic liquidity management decisions has a bearing on the systemic level. Ratnovski and Huang (2009) examined the factors shaping the resilience of Canadian banks and noted that less reliance on wholesale funding than their peers in other advanced countries helped them. Demirguc and Huizinga (2009) found that the banks' reliance on non-deposit sources of funds made them more vulnerable. Rajan (2006) observed that banks' greater reliance on market liquidity caused risk to their balance sheets in times of crisis.

Most of the studies so far have primarily focused on the institution-specific factors for explaining the liquidity conundrum. However, a causal relationship so as to understand the manifestation of systemic liquidity risk has not been examined possibly with reference to the macroeconomic data of endogenous and exogenous factors in the context of a developing economy. While at the idiosyncratic level a number of factors could be responsible for a bank's specific liquidity crunch, it is far more important and useful to understand the manifestation of the liquidity risk at the systemic level as a result of interaction of individual liquidity risk components. Second, the significance of price stability, ceteris paribus, for the systemic liquidity in the context of developing economies has not been fully explored. Third, the question relating to the asymmetric movement of systemic liquidity is very interesting and important from the policy perspective. The question as to whether the systemic liquidity risk is more pronounced in recessionary conditions or during inflationary phase needs empirical evaluation to examine a possibility for the existence of a zone of stability. This study intends to examine the above three questions and find possible explanations in terms of a simple yet robust macroeconomic model of systemic liquidity which could work quite smoothly with minimal complexity and a high degree of significance.

The challenge is to use and relate the macroeconomic data to understand and mitigate the liquidity conundrum. In general, the systemic liquidity management resonates between absorption and injections as conditions evolve from surplus and shortage at the macro level. A macroeconomic evaluation of systemic liquidity risk from the perspective of developing economies, therefore, hinges upon the following four risk parameters:

• Frictional liquidity risk occurs due to the interaction between the transient factors, such as periodic tax collections, volatile government receipts, large one-time receipts/payments or inflationary spirals.
• Structural liquidity risk is caused by the widening difference between the credit pick-up and the deposit growth in the banking system coupled with the movement in the currency in circulation.
• Funding liquidity risk is the risk that the counterparties who provide the short-term funding might withdraw or not roll-over the funding.
• Market liquidity risk is the risk of a generalized disruption in asset markets, thereby making otherwise apparently liquid assets illiquid.

The frictional and structural liquidity risks are manifested in the form of funding liquidity risk and also the market liquidity risk. Both of these could precede and succeed each other depending on the prevailing macroeconomic scenario. Interactions of the above four risk parameters define and shape the liquidity risk at the systemic level.

Systemic Liquidity

The maintenance of an adequate level of systemic liquidity consistent with its ultimate goals of price and financial stability is of paramount importance for an economy. At the same time, it is also critical that the banks and financial institutions adopt prudent liquidity management systems and have adequate liquidity buffers to ward off any possible liquidity crisis, as the huge reputational risk that is propagated by the liquidity crisis could have serious negative repercussions for financial stability. Figure 1 presents a schematic view of the manifestation of systemic liquidity risk.

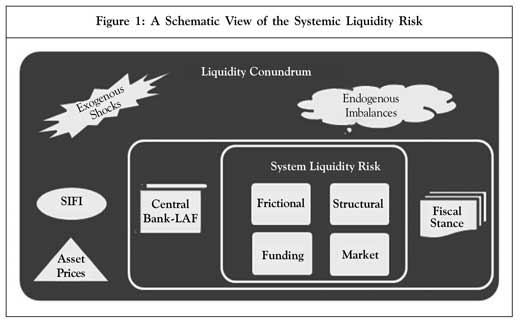
The macroeconomic factors affecting the systemic liquidity scenario could emerge from exogenous shocks or endogenous imbalances. While the exogenous shocks of the magnitude of the global financial crisis of 2008 could seriously threaten liquidity in the affected economies, even the endogenous imbalances prevailing in the financial system could also jeopardize the financial stability and systemic liquidity equilibrium. Though the manifestation of systemic liquidity risk could take different forms and patterns, the systemic liquidity risk and threat to financial stability become more pronounced both in the case of recession (rather a depression) and hyperinflation.

The liquidity conundrum is manifested both in the case of sudden shrinkage in the economic activities, as explained above in the case of external shocks. In this situation, the systemic liquidity risk originates from a worsening of the market liquidity which leads to funding liquidity risk and subsequently assumes the structural dimension. Due to the limited role of a frictional component of liquidity risk, in this case, the job of restoring normalcy becomes quite tedious for the central bank. While the short-term liquidity adjustment by the central bank could manage the frictional nature of the liquidity risk, the structural dimension of systemic liquidity risk demands enduring management and also active support from the fiscal front. A more challenging and rather subtle form of systemic liquidity risk stems from an overheating economy, especially when the source of overheating is centered on the comparative illiquid asset classes, such as property, gold or other speculative investments. In the context of developing economies, a certain involvement of the so-called black money also plays a hand in the overpricing of assets and underpricing or risks. Apparently, this signals a false impression of growth, but in reality, this brings in a vicious cycle of poor credit. Such a vicious cycle severely impacts the banks and borrowers alike. A hardening of interest rates leads to shrinkage of funding liquidity which then spills over to the market liquidity risk. Though the liquidity conundrum, in this case, remains mostly frictional, if sustained, it could also assume a structural dimension. Systemically important financial institutions (SIFI) play a critical role in the entire episode along with the monetary and fiscal stance. Policy transmission mostly happens through interest rates and asset price channels with their natural time lags. It is important, therefore, to understand the macroeconomic factors which could be monitored to assess the liquidity risk at the systemic level.

The unsecured segment of the inter-bank call money market sets the weighted average call rate (WACR) on a daily basis, which is the operating target of monetary policy in India (Pattanaik et al., 2017) and hence, could be used as a proxy indicator for liquidity risk. By modulating liquidity conditions, the Reserve Bank of India (RBI) aims to anchor the WACR around the policy repo rate and therefore the movement of WACR above the policy repo rate could be used as an indicator of liquidity stress at the systemic level. An excess of WACR over the repo rate could be considered as the liquidity risk premium.

In case the WACR is used as the dependent variable, as a proxy indicator for systemic liquidity risk, the choice of independent factors (variables) should be the most relevant macroeconomic factors defining all the four components of systemic liquidity, namely, structural, frictional, market, and funding liquidity. To illustrate, variables defining the structural liquidity (such as credit growth, deposit growth, reserve money growth), frictional liquidity (such as bank and central government cash balances), market liquidity (such as gold, property, stock prices, as also the wholesale price growth), and funding liquidity (such as repo rate, benchmark 10-year government bond yield), etc., could be used as independent variables having an influence over the WACR, the dependent variable. The impact of repo operations under the LAF, though quite important, is expressed in the frictional liquidity variables and hence, should not be used as an independent variable.

It could be observed from Figure 2 that during the last five years, the WACR has mostly remained aligned with the policy repo rate, except for occasional liquidity spikes and a period of liquidity stress during July-December 2013 when the WACR substantially moved upward, notwithstanding the heavy injection of liquidity under the LAF. On a long-term basis, the systemic liquidity risk was contained around the policy corridor and the periods of liquidity stress were characterized by macroeconomic issues, such as inflationary pressures and volatility in the foreign exchange market. During the recent past, the LAF has mostly remained in

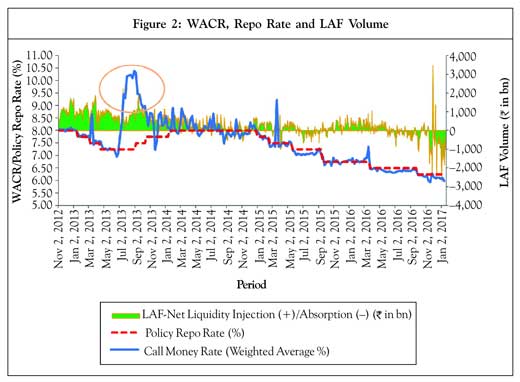
absorption mode and the call rates not only fell in line with the policy repo rates but were hovering slightly below the policy rates, indicating a comfortable position of the systemic liquidity. One of the major macroeconomic factors responsible for such a cushion was possibly the high-value banknote demonetization move by the Government of India on November 8, 2016, thereby demonstrating the impact of macroeconomic factors on systemic liquidity.

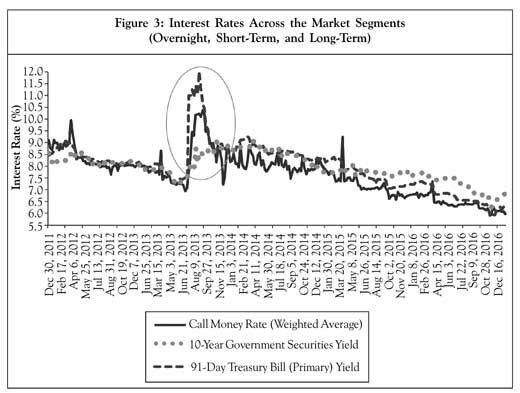
However, this is not to suggest that the institution-specific factors do not impact on liquidity at the systemic level. For instance, in India, the final guidelines1 on the Liquidity Coverage Ratio (LCR) under Basel III liquidity are under phased implementation and the banks have had to comply with a minimum starting requirement of 60% from January 1, 2015, 70% effective from January 1, 2016, and 100% norm by January 1, 2019. Pattanaik et al. (2017) observed that the LCR constrained banks altered their activity in the call money market and borrowed at a higher rate, due to which the WACR was pushed up by 5 to 7 bps. A more secular reflection of the liquidity situation is indicated in Figure 3. It can be seen that the 10-year benchmark government security yield, though mostly aligned with other rates, was far more stable than the short-term rates. This is quite natural since the liquidity situation, as an essentially a short-term phenomenon, is much better reflected by the weighted average call money rates, though not much influenced by the idiosyncratic factors.

Objective

This paper attempts a macroeconomic evaluation of the systemic liquidity risk from the perspective of developing economies. It analyzes the relevant macroeconomic variables in order to design a simple though robust empirical model to explain the variation in the WACR against the significant variables as regressors over a sufficiently long period of time.

Data and Methodology

As a test case, the relevant macroeconomic data from the Indian financial system has been used for the purpose of analysis over a sufficiently long period of time from 1970-71 to 2015-16 thereby using 46 annual time series observations. Ordinary Least Square (OLS) – HAC standard errors and covariance method is used along with the test for stationary variations. Figure 4 represents the movement of WACR against the repo/bank rate on the left axis along with moving-average of commercial bank and central government balances on the right axis during the period 1970-71 to 2015-16. It can be observed from Figure 4 that a significant liquidity risk premium (excess of WACR over the repo/bank rate) prevailed in the market for a sustained period during 1974-75, 1991-92 and 1995-96. The reference made to the exogenous and endogenous macroeconomic variables earlier in the paper explains the phenomenon. While the situation prevailing in 1974-75 was primarily a result of external oil price shock2, the later periods of liquidity stress were the manifestations of internal imbalances in the economy (the Balance of Payment (BoP) crisis3), a rapid monetization of the economy during the last 15 years is also apparent.

Macroeconomic Model Estimation

A number of critical macroeconomic variables were examined to develop a suitable regression model to establish a causal relationship and find useful explanations about the systemic liquidity risk. Some of the variables, such as the gross fiscal deficit, current account deficit, growth in capital, and gold and illiquid asset prices, were initially considered but were not found significant, either due to strong multicollinearity with other independent variables or due to a lack of comparable data. Since no strong feedback loop is present in the exogenous factors, OLS technique could indeed be used. After examining the suitability of various estimation variables, the following model was developed as a simple, robust and significant causal OLS regression model. The variables used are as follows:

CALL_WTD = Weighted average interbank call money interest rate (WACR) M0_GR = Annual growth in the reserve money (%) (Currency in circulation + banker's deposits with the RBI + other (FI) deposits with RBI) WPI_GR = Annual growth in the wholesale price index (%) (Proxy for inflation) CRR = Cash Reserve Ratio4 (%) SLR = Statutory Liquidity Ratio5 (%) CR_GR = Annual growth in the commercial bank's credits (%) DEP_GR = Annual growth in the commercial bank's deposits (%)

Considering the nature of variation and data generating process, a non-linear cubic variable transformation was attempted with respect to variation in the wholesale price index and an interaction between deposit growth and credit growth rates was used as regressors. The following are the estimation equation and the substituted coefficients:

Estimation Equation:

Results and Discussion

The regression results are presented in Table 1. It is observed that the overall model is significant. The F-statistic is 7.97 and its p-value is 0.000003, which is much smaller than 0.05. All the variables including the intercept are significant at 5% except for the cubic transformation of WPI_GR, which is significant at 10%. The p-value of the Wald F-statistic is 0.00 and hence, all the variables are jointly significant. R2 of 0.67 indicates that about 67% of the total variation in WACR is explained by the model. Adjusted R2 of 0.59 is not too far from the R2 and hence, the inclusion of additional regressors has not reduced the explanatory capabilities of the model. The SE of regression at 1.83 is lower than the SD of the dependent variable at 2.85. Based on the influence statistic, one of the most influential observations was omitted so as to ensure a fair estimate.

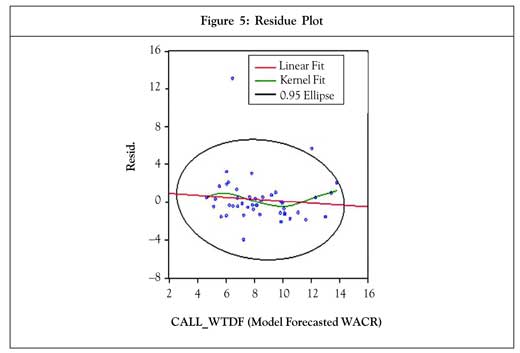
The residue appears to be evenly distributed within the 95% confidence ellipse across the fitted WACR (Figure 5) and hence meets the requirement of a zero conditional mean for OLS estimation. The model also passes the functional form Ramsey RESET test. The p-value of F-statistic is 0.22, which is well above the significance level of 5%.

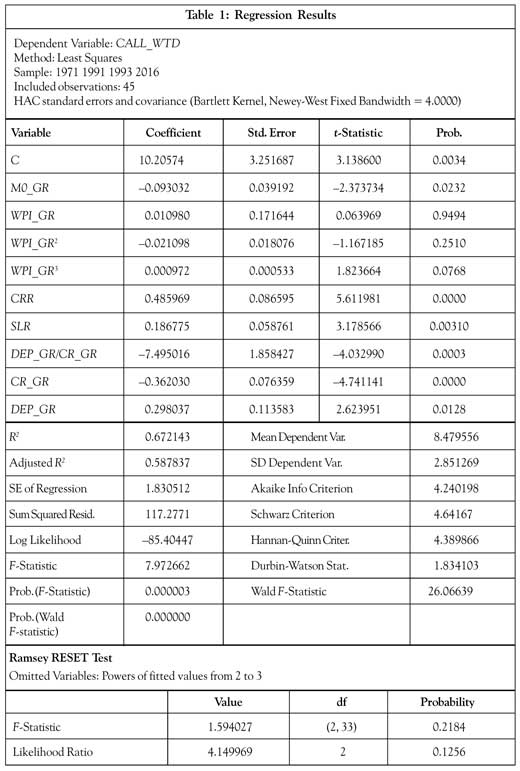
The model provides a very useful insight into the causal relationship of systemic liquidity with significant macroeconomic variables. An expansion of 1% in the reserve money (M0) reduces the WACR by 0.09%. An increase of 1% in both the CRR and SLR reduces the liquidity and adds 0.49% and 0.19% to the WACR, ceteris paribus, respectively. A very interesting inference is obtained from the ratio of deposit growth to credit growth, which explains a downward adjustment of 7.50% from the intercept when the deposit growth is exactly equal to the credit growth. In situations where deposit growth is higher than the credit growth, the systemic liquidity improves with a fall in the WACR. On the contrary, if the credit growth outplays the deposit growth, the systemic liquidity comes under stress as indicated by an increase in the WACR.

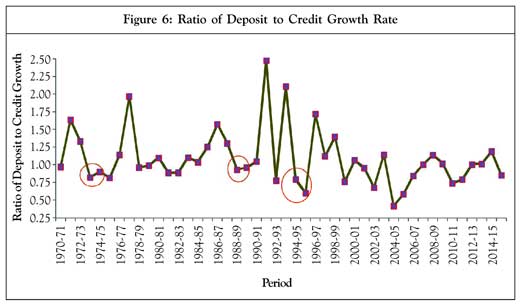
It can be observed from Figure 6 that the periods of liquidity stress as indicated in Figure 4 were preceded by a fall in the ratio of deposit to credit growth rates (1972-73, 1988-89, and 1994-95)—the ratio remained much less than one.

In this model, the impact of inflation (growth rate of WPI), ceteris paribus, on the systemic liquidity as measured by the movement in WACR is explained as follows:

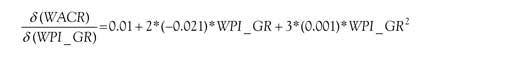
The model predicts that a worsening of systemic liquidity is more pronounced in recessionary conditions than during inflationary conditions and a moderate level of inflation does not cause any liquidity stress, but on the contrary, it helps in easing out the liquidity risk. The liquidity is more threatened in a recessionary environment, but on the other hand a similar degree of threat occurs only during a very high inflationary situation. Figure 7 shows the variation in the WACR against the movement in WPI. The model predicts a zone of stability or low risk to systemic liquidity when the rate of growth in the WPI remains positive up to 14%. However, beyond that, a further rise in inflation fuels the rise in WACR. This establishes the fact that a controlled inflation acts as a growth anchor for developing economies, ceteris paribus. The model successfully establishes that the systemic liquidity becomes endangered both in recessionary and overheated economic conditions.

The relationship also shows that the systemic liquidity as reflected by the WACR in the model is best served when there is no significant variation in the inflation, which means that the prices are stable at a reasonable level. This is fairly consistent with the premise that price stability is a prerequisite for financial stability as adequate systemic liquidity is an integral part of the financial stability doctrine. Conclusion In a nutshell, the above macroeconomic model of systemic liquidity works quite smoothly with minimal complexity and a high degree of significance. The regressors, including the intercept, successfully explain the causal relationships so as to understand the manifestation of systemic liquidity risk. The importance of deposit growth against credit growth for systemic liquidity is highly relevant from the perspective of developing economies. Moreover, the model at 10% significance demonstrates that systemic liquidity risk could be mitigated to a large extent by ensuring price stability. Since other significant variables, namely, the CRR and SLR are used as policy tools to ensure price stability, a lower systemic liquidity risk premium depends to a great extent on the stable prices and well anchored inflationary expectations. To summarize, this paper shows that structural and frictional liquidity risks shape systemic liquidity risk through the channels of funding and market liquidity risk. It is, therefore, quite useful both for the market participants and the central bank to keep a close watch on the interaction among these risk parameters so as to better understand and mitigate the manifestation of systemic liquidity risk. v References